GRRM 1.22

　化学は、100種類ほどの元素を素材にして、多種多様な物質をほとんど限り無く組み立てることのできる、希望に満ちた楽しい世界です。人類が手にした化合物の数は、1965年に約25万種であったものが、今では3000万種にまで達し、毎年200万種ずつの割合で新化合物が誕生しています。そして、化合物どうしを結ぶ化学反応について、化学者達による発明や発見がとめどなく繰り広げられているのです。

80年ほど前に量子力学が誕生したことによって、化学の問題は理論的に解決したかに見えましたが、実際には解くべき方程式が複雑過ぎて、簡単に解くことができなかったため、量子力学によって化学の問題を解くもくろみを捨てる人が続出しました。その中で理論化学者達は、化学の問題を量子力学によって解決する夢を持ち続け、近似理論の改良を根気良く続けるとともに、急速に発展した電子計算機の技術を活用して、次第に量子力学に基づく問題解決の範囲を拡大して行きました。

　現在は、量子化学計算プログラムを用いて原子の集団がその幾何構造に依存して変化させるエネルギーの極小を求めることで、実験しなくても、分子の構造やエネルギーを、かなり精密に決定するこができます。専門家はこの作業を構造最適化と呼んでおり、今では誰でも日常的に行うことができますが、この作業には初期推定という予備作業が必要であり、これはコンピュータを使う我々が経験や化学的直感に基づいて行わなければなりません。初期推定をうまくやる一般的な方法は確立されていないため、新化合物や新反応ルートを構造最適化によって理論的に見つけ出すためには、試行錯誤に頼らざるを得ません。このため、同じ化学式で表される異性体を調べ上げ、それらの間の反応経路を解明することは、わずか４原子からなる化合物についてしか達成されておらず、５個以上の原子からなる化合物については、まったく未踏の頂だったのです。

　この前人未到の頂を目指して2004年に大野・前田の超球面探索法（SHS法： Chem. Phys. Lett. 384, 277 (2004))が開発されました。これは任意の化合物の構造を出発点として、その周りに存在する反応経路を探り当て、それらの反応経路を１つずつ辿ることで、他の異性体への反応経路や解離反応経路を見つけ出し、新たにみつかった異性体の構造から、同様の操作を芋づる式に繰り返すことで、同じ化学式で表される異性体とそれらに繋がる反応経路を自動的に暴き出すことを初めて可能にしたのです。

　大野・前田のSHS法では、任意の構造からその周囲へと向かう反応経路が、平衡点付近の放物線型のポテンシャル（調和ポテンシャル）から、必ず下方に歪んでいること、すなわち、化学反応経路は非調和下方歪みに沿って展開すること（化学反応の量子原理：J. Phys. Chem. A 110, 8933 (2006)）に着目することで、安定構造から始まる化学反応経路を見つけて追跡することを初めて可能にしました。化学的な構造が示すポテンシャルの非調和下方歪みが示す方向が、目印や道標の何もない海洋上で南北を指し示す羅針盤のように、どちらに行けば反応が進むかを示す「化学の世界の羅針盤」のような働きをすることが発見されたのです。

　化学反応を扱う伝統的反応理論として、Bell・Evans・Polanyiの原理(1936年)、福井のフロンティア軌道論(1952年)、Hammondの仮説(1955年)、Woodward-Hoffmann則(1969年)、Marcusの式(1968年)などが有名ですが、いずれも簡潔なモデルを利用していて、精密なポテンシャルエネルギー表面の山あり谷あり峠ありといった非常に起伏に富んだ形状に直接アッタクするものではありませんでした。

　この数十年の間に、量子化学計算の信頼性が向上し、ポテンシャルエネルギーが化学的精度で計算できるようになったため、伝統的反応理論を超えて、化学反応の予測や解析を量子化学計算に基づいて自動的に行う方法の確立が待望されるようになりました。

　

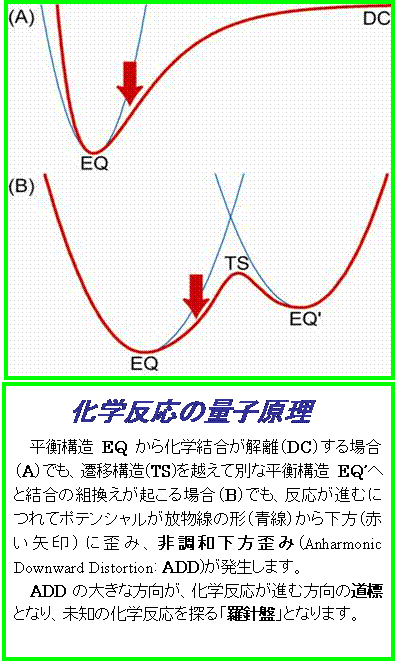
ポテンシャルの非調和下方歪みに着目する「化学反応の量子原理」は、量子化学計算に基づいて化学反応をコンピュータで自動探索することを初めて可能し、無限の可能性を秘めた未知の化学の世界を探検するための「羅針盤」となって、化学者の夢の実現を強力にサポートします。　　

　 とは

○ GRRM 1.22は、グローバル反応経路マップ（Global Reaction Route Map : GRRM）を、量子化学計算に基づいて自動的に探索する世界初のプログラムです。

○ GRRM 1.22は、指定された化学式で表される異性体とそれらを結ぶ異性化反応経路および分解反応経路を自動的に探索します。

○ GRRM 1.22は、自動的に探索された反応経路上の遷移構造を決定し、極限的反応経路（IRC）および遷移構造での基準振動と虚数振動数を求めることができます。

　　

○ GRRM 1.22は、まだ誰にも知られていない新化合物や新反応ルートを効率よく自動的に探索することを可能にし、未知の化学の世界への扉を開いてくれます。

○ GRRM 1.22は、シラミツブシに調べるやり方では何兆年かけても分からないことを、閉じた曲面で包囲しながら「化学反応の量子原理」に基づいて探す「超球面探索法」によって、非常に効率的に新化合物や新反応ルートを見つけ出してくれます。

○ GRRM 1.22は、作りたい物質の分解経路を調べてその逆の合成経路を見つけることができるため、資源をまったく無駄にせず余計な副産物をまったく残さない理想的な反応経路（Atom Economy）を設計することができ、省資源と環境保全に貢献します。

○ GRRM 1.22は、経験や直感をまったく必要とせず、誰にでも使うことができ、指定した化学式で表される化学種とそれらを結ぶ反応経路を自動的に暴き出してくれます。

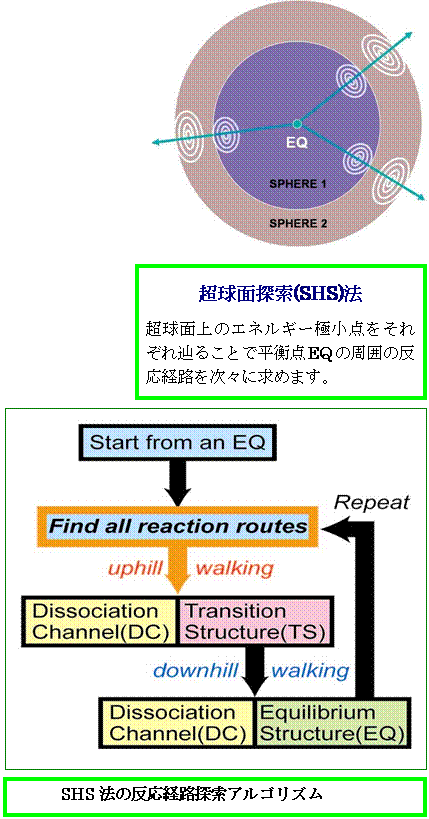
◎ なぜこれまで、グローバル反応経路マップGRRMの自動探索が不可能だったのでしょうか？　それは、安定な構造（EQ: 平衡構造）から出発する反応経路を全て見つけ出し、それらの経路をエネルギーが上昇する方向に辿って遷移構造(TS)や解離構造(DC)を見つけるアルゴリズムが存在しなかったからなのです。GRRM 1.22では、大野・前田の超球面探索法(Scaled Hypersphere Search Method : SHS法)によって、この問題をはじめて解決し、GRRMの自動探索を実現しました。

◎ SHS法では、どのようにして、平衡構造からその周囲に繋がる反応経路を全て見つけ出すことができるのでしょうか？　

それは、「化学反応の量子原理」に基づいています。化学反応のポテンシャルの特徴を調べてみると、平衡構造の付近は、調和ポテンシャルとよばれる放物線の形をしていますが、反応が進むにつれてポテンシャルが必ず放物線の形から下の方に歪みはじめています。すなわち、ポテンシャルが反応の進行に伴って調和的ではなくなり非調和的下方歪（Anharmonic Downward Distortion : ADD）を発生しています。これが化学反応の量子原理であり、ADDの大きい方向が化学反応の進行方向を示す羅針盤の働きをもつのです。この原理により、ADDが大きい方向をみつけて辿ることで平衡構造からの反応経路の追跡が初めて可能になったのです。

◎ SHS法は、化学反応の進路となるADDが大きな方向を非常に効率よく見つけます。

　　ADDの極大を見つけるのにポテンシャルが最も下がる方向を探すのは誤りです。これは一番振動数の低い基準振動モードに引きずられてしまい、これではADDの極大は見つけられません。ポテンシャルの非調和性は、３次以上の高次項が関係するので、高次の微係数を求めて行けば原理的には可能なはずですが、高次微分を求めるのにコストがかり、それらを使ってADDの極大方向を定めるにも莫大なコストがかかってしまいます。

そこで、SHS法では、規格化した基準座標を導入することで、基準振動の振動数の違いを消し、全ての基準座標を同等に扱います。規格化された基準座標系では、ポテンシャルが仮に完全に調和的であったとすると、平衡点から等距離の超球面上でのエネルギー値はどの方向もみな等しくなります。実際のこの超球面上でのエネルギー値はポテンシャルに非調和性があるため方向によって違ってきます。そこで、超球面上で実際のエネルギーの極小を求めて行けば、各極小点の方向がADD極大の方向であり、平衡構造の周りに存在する反応経路が次々に求まります。

◎ SHS法では、閉曲面で囲んでADDの極大を探すことによって、１つの化合物からその周囲につながる反応経路を自動的に見つけ出すことを初めて可能にしました。この閉曲面は１組だけ０から２π、他は０からπの間の値だけが許される変数で記述される有限な領域であるため、無限の試行錯誤を要さずに探索することができます。このように、SHS法では、閉じた領域に限定して探すことで、その領域を出入りする反応経路を自動的に効率よく捉えることができるのです。

◎ GRRM 1.22では、超球面上のエネルギー値の極小（ADDの極大）を全て求めると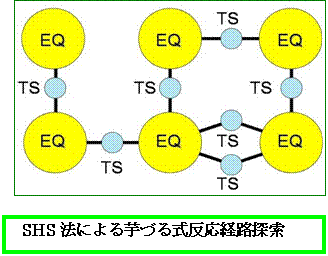ころに特別な技法を導入し、これまで不可能であったことを実現しています。

　　量子化学計算でエネルギーが極小となる構造を１つ見つけるのは、構造最適化と呼ばれる方法で比較的容易に行えます。しかし、全部の極小を求めるとなると簡単ではありません。これは、超球面上に範囲を限ったとしても、普通のやり方では、ほとんど不可能になってしまいます。　

この問題は、前田・大野の逐次最適化消去法（IOE法： J. Phys. Chem. A 109, 5742 (2005)）によって解決されました。超球面上の極小近傍の形が余弦関数を用いて表されることを利用して、一度極小を見つけたら、その「穴（極小）」を埋めてしまうことで、未発見の「穴（極小）」を、構造最適化と同様の手続きで、次々と見つけることができるのです。

◎ SHS法に付随して開発されたIOE法には、さらに凄まじく優れた威力があります。実は、反応の進行方向を示すADDは、反応経路どうしが互いに接近すると重なって、独立した極大とはならずに肩のような形になってしまうことがあり得ます。でも大丈夫なのです。IOE法では、複数の反応経路が重なってできたADDの極大は簡単にみつかるのでそれを取り除いてしまうと、その下に隠れていた別の反応経路のADDが新たに極大となって現れてくるので、近接して隠されてしまった反応経路も難なく見つけ出すことができるのです。この操作は、いくつかのピークが重なって複雑な形をしたスペクトルから個々のピークを暴き出す分光データ解析手法（デンコンボルーション技術）と大変よく似ています。目で見てもわからないようなスペクトル成分がコンピュータを使った解析で見事に出てくるように、GRRM 1.22にも、近接する反応経路の互いに重なったADDを自動的に分離し、それぞれ別々な反応経路として検出する技術が搭載されています。